面向 PPT 的自控复习 ​

复习资料：PPT 自控英文书 自控中文书

第一次尝试面向 PPT 复习，主要思路是以 PPT 为骨架，然后用书籍、资料和练习进行血肉的补充。

重点会使用引用的形式标出来

1 ​

Controller sensor actuator ref

3 ​

7 The Root Locus Method ​

7.1 What is a Root Locus ​

回忆一下特征方程，特征方程只在闭环中出现。这里的特征方程是默认反馈的增益为 1 的。

特征方程: $1+KG(s)=0$

注意，K 始终为自然数

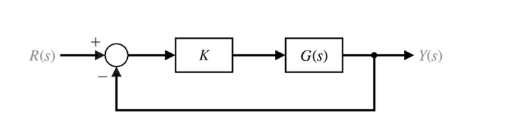
Root locus 方法是画出在 K 变化时的根轨迹。根指的就是闭环极点。

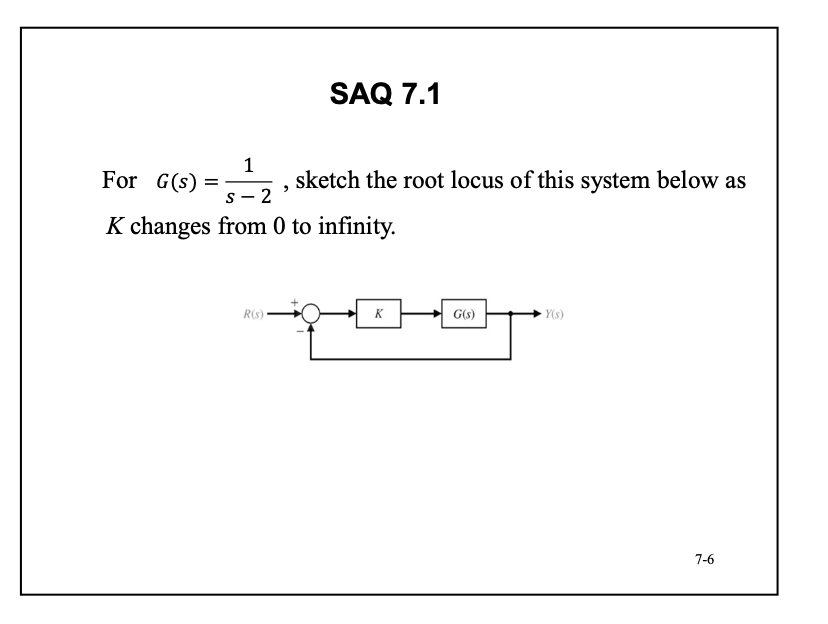
画出来是一条直线

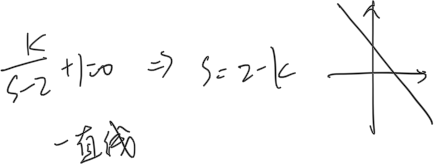
7.2 Root locus Procedure ​

步骤一：解特征方程

根轨迹本质上是在解方程，所以首先列出特征方程，根据特征方程做文章。

以下是第一个步骤

1. $1+KG(s)=0$
   • $G(s)$ 分解
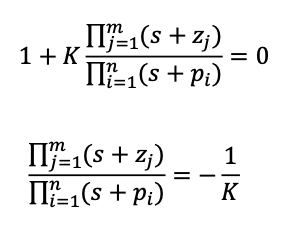
   • 在图中画出零点和极点
     • 零点画 o 极点画 x
   • 画出 separate loci
     • 从 n 个极点画到到 m 个零点，其他的点直接飞走，飞到无穷
     • 所以有(n-m)个 branches
   • the root loci are symmetrical with respect to the horizontal real axis
     • 这是由于在分解传递函数的时候复数根总是成对出现。可以想一想初中解二次方程的时候，那个正负根号 4ab 是虚数项。事实上，实高次方程总可以拆成根相乘的形式，没有实数解的总会由两个共轭复数解凑出来

$ G(s) $ 是开环传递函数，所以有零点和极点。根据回忆，零点和极点都是由于拉普拉斯方程中微分和积分项的存在，所以我们是在根据开环的方程来描述闭环的表现。如何保证开环和闭环是单映射呢？我们其实简化了方程

那对于那些反馈不是常函数的系统呢？

在 K 趋向于 0 的时候，只有极点会起作用；在 K 趋向于$\infty$ 的时候，只有零点会起作用。所以在画根轨迹法的时候，总是由极点画到零点。这点非常重要，似乎是一个趋势。

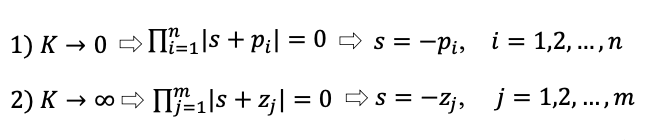
步骤 2：实数轴连点成线

这个情况我觉得是假设有实数根的情况下一定符合，但是仍然是有很多问题的。

第一，假如很多极点连续的排列在实轴上呢

第二，为什么一定是往负方向走？

步骤 3: 渐进线

由步骤 1 可以看出，渐进线是由于飞走的 branch 产生的。所有的渐进线都交于实数轴上的一个点。

为啥是一个点？

这个点是

σ​a​​=​n−m​​∑​i=1​n​​(−p​i​​)−∑​j=1​m​​(−z​j​​)​​

注意符号，带负号的才是零点和极点。还有是极点减去零点，就跟分母一样，因为分母总是比分子高次。

一个点分出来了很多条渐进线，公式是

θ​a​​=​n−m​​(2k+1)π​​

$$k=0,1,2...(n-m-1)$$

把 n-m 带入这个公式，会发现很有意思的事情。在 n-m=0 的时候没有意义。大于 1 的时候总会有渐进线走向实负轴。然后剩下的事实上是在平分这个平面。

这个时候 PPT 展示了一张狗屎推导。

事实上是这俩公式的推导，可看可不看。

步骤 4: 确定 locus 路过虚轴上的点

乱飞的 branch 有时会碰到虚轴，我们为什么要确定虚轴上的点呢，因为这是稳定性的阈值。

本质上也是在解特征方程，然后把$s$全部替换为$j\omega$

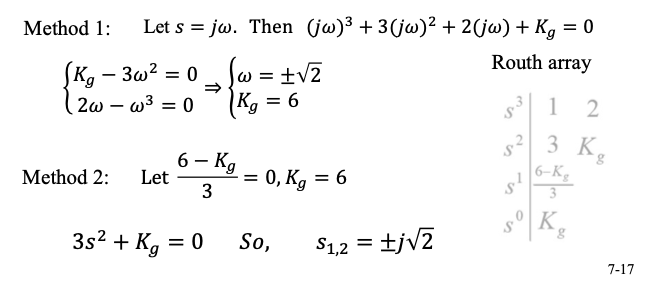
步骤 5: determine the breakaway point on the real axis

刚刚确定了渐进线的交点，但是真正的 locus 是在哪里分离的呢，就是 breakaway point。

还是解特征方程，把 K 写作 s 的方程

然后导数为 0，就可以得到分离点了。

​

步骤 6: 画出出发和到达的角度

不在轴上的点怎么处理？从极点出发，到达零点都有一个角度，这个角度让我们相对于实轴进行。

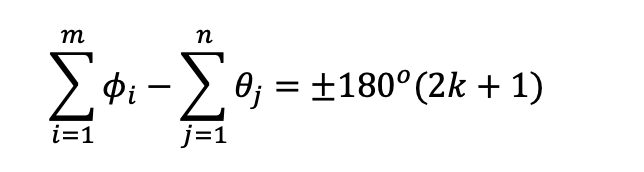
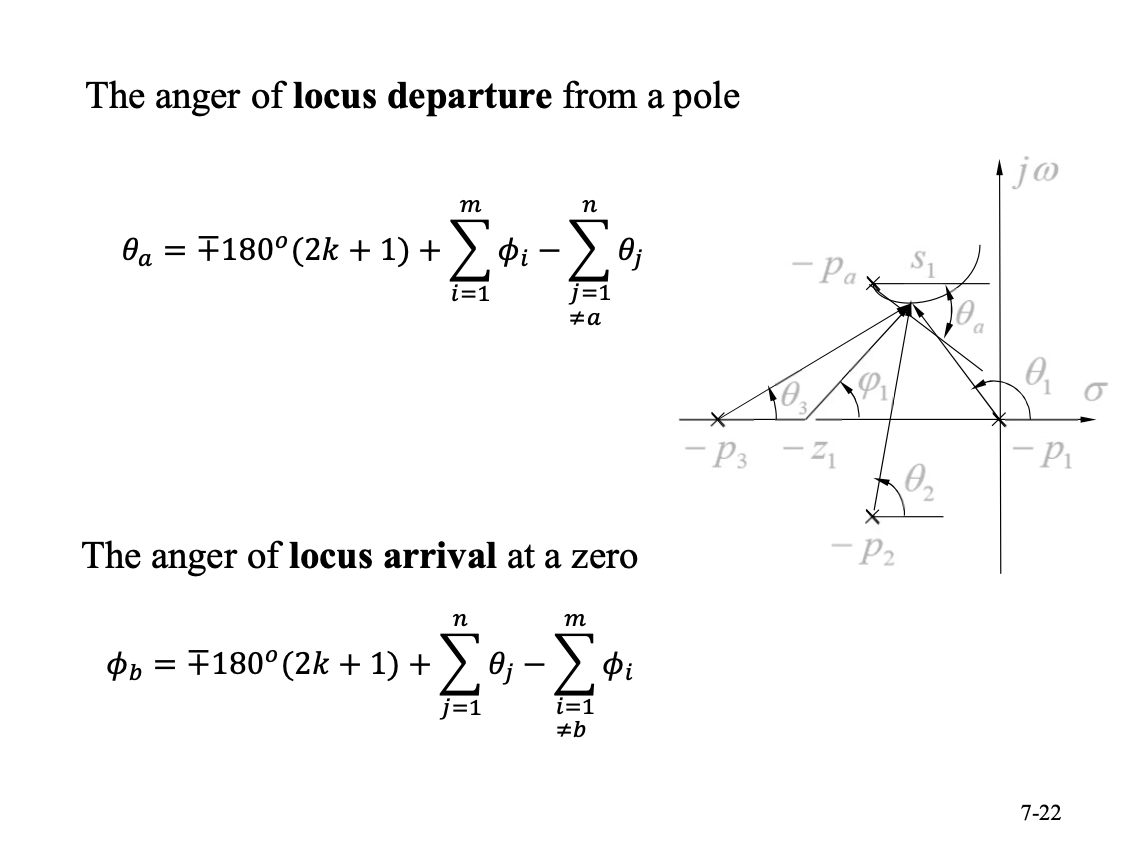
这张 PPT 讲的其实很清楚了，假如你是零点，就正负 180 度加上极点减去其他零点，然后转化到正负 180 度以内好画出来。

**这里有一个问题，就是 180 度的问题，决定了到你这来的方向，目前还没有看到讲解?**我倾向于你在虚轴上方就是加 180 度，在虚轴下方就是减 180 度

步骤 7: 结束！

接下来是连点成线，手画或者 matlab

然后是判断一个点在不在你的根轨迹上，

相位法：

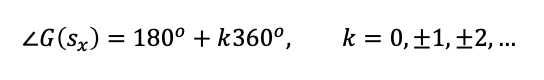
在轨迹上的点显然都满足这个条件。

但是是不是所有满足这个条件的点都在直线上？ 我暂且认为是对的。

然后是判断你的一个点上的 K 值

K​x​​=​∏​j=1​m​​∣s​x​​+z​j​​∣​​∏​i=1​n​​∣s​x​​+p​i​​∣​​

注意 p 在上，z 在下，别搞反了。K 始终和极点在一个位置。

特殊的根轨迹

• arc root locus

挺好玩的。

• Parametric 根轨迹

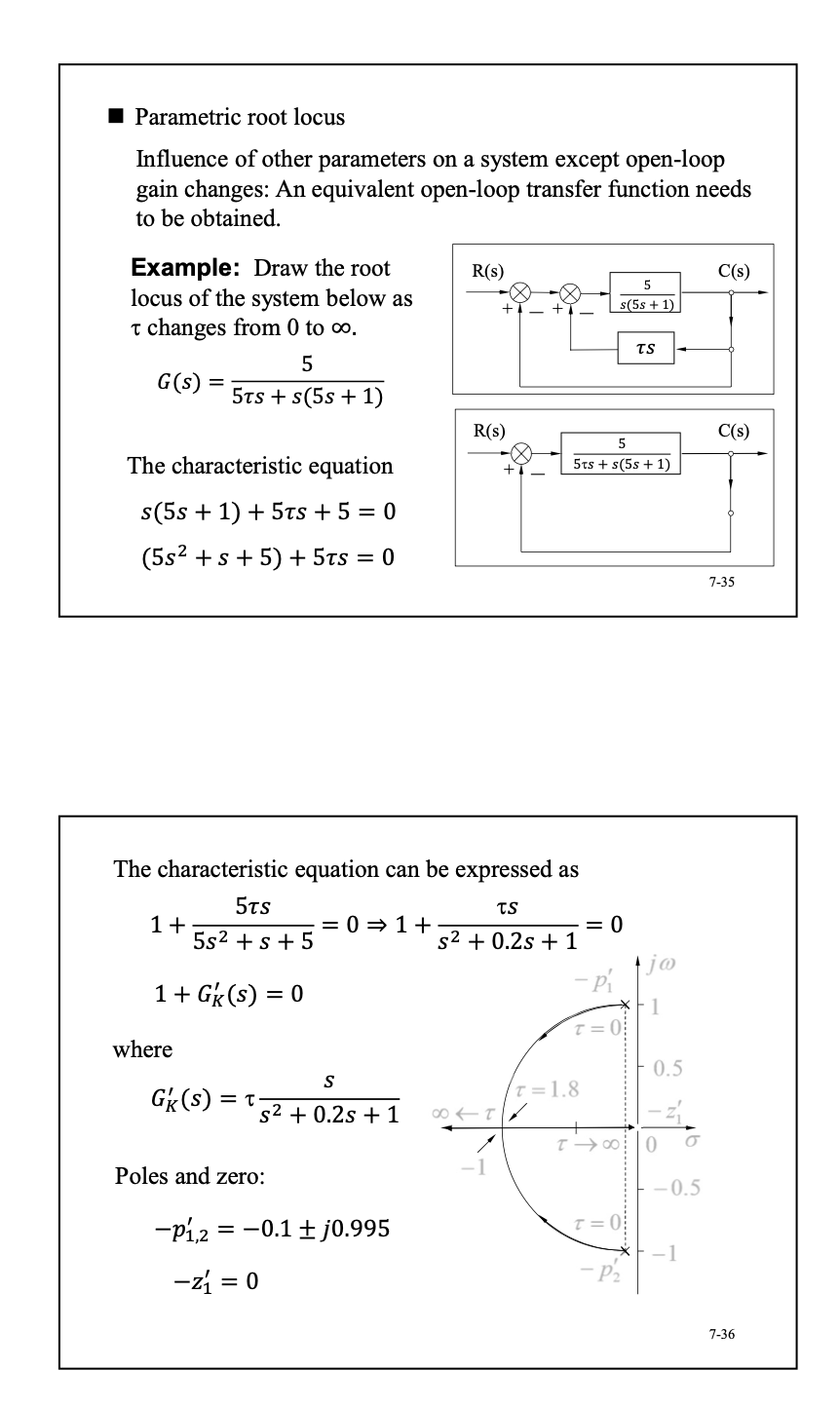
7.3 Properties of Root Locus ​

8 PID Control ​

P control ​

u(t)=K​p​​e(t)

M(s)=​1+K​p​​G(s)​​K​p​​G(s)​​

注意这个 e 不是指数

然后

PI controllers ​

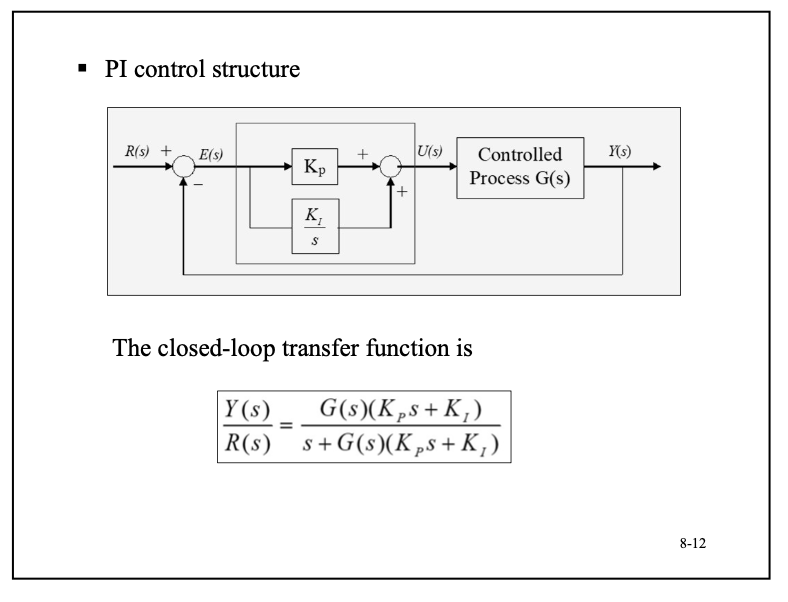
突然想到，很多时候要做到计算效果带宽有关系

PD Control ​

Ziegler-Nichols Oscillation Method